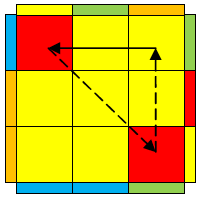
OPLL

From Speedsolving.com Wiki
OPLL
Information
Proposer(s): unknown
Proposed: unknown
Alt Names: Lazy ZBLL, MOPLL
Variants: none
Subgroup:
No. Algs: 21 unique with setup moves(PLL algs)
Avg Moves: 14.3 HTM
Purpose(s):

OPLL, also known as lazy ZBLL is a subset of the ZBLL last layer method that caan be solved with conjugate PLL's. So no new algorithms need to be learned if you already know PLL (Conjugate is [A B A']).

Please note that because not everyone uses the same PLL's, the first listed case may not work for you. Because of this, the PLL is listed inside the brackets, feel free to subsitute it.

Notes

There may be some AUF's or rotations involved in certain cases which will be listed below.

For G-Perms I hold the block in the Front.
For R-Perms I hold the block so that the corner of the block in in the front-right or front-left.
For F-Perms I hold the solved side in the front.

OPLL

Bowtie Cases | Headlight Cases | Chameleon Cases | Other Cases| edit

See also

OPLL algorithms

Note that all of these algorithms assume that you are right-hand dominant and know the Western notation, where a lowercase letter means a double-layer turn and rotations are denoted by x, y, and z. (how to add algorithms)

Click on an algorithm (not the camera icon) to watch an animation of it.

Bowtie Cases

A-perms

Name: B(A-f)
Used in: ZBLL,OPLL
Optimal moves: (Aa+2)HTM
{{{text}}}

OPLL F (R' F R' B2 R F' R' B2 R2) F’

Name: B(B-f)
Used in: ZBLL,OPLL
Optimal moves: (Ab+2)HTM
{{{text}}}

OPLL F’ (R B' R F2 R' B R F2 R2) F


G-perms

Name: B(Gb-f)
Used in: ZBLL,OPLL
Optimal moves: (Gb+2)HTM
{{{text}}}

OPLL F' (F' U' F R2 u R' U R U' R u' R2) F

Name: B(Gd-f)
Used in: ZBLL,OPLL
Optimal moves: (Gd+2)HTM
{{{text}}}

OPLL F (F U F' L2 u' L U' L' U L' u L2) F'


J-Perms

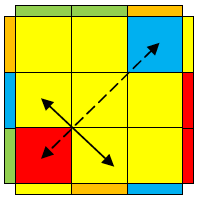
Name: B(L-b)
Used in: ZBLL,OPLL
Optimal moves: (Ja+2)HTM
{{{text}}}

OPLL B (L' U2 L U L' U2 R U' L U R') B'

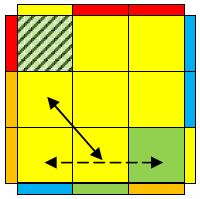
Name: B(L-l)
Used in: ZBLL,OPLL
Optimal moves: (Ja+2)HTM
{{{text}}}

OPLL L (L' U2 L U L' U2 R U' L U R') L'

Name: B(J-b)
Used in: ZBLL,OPLL
Optimal moves: (Jb+2)HTM
{{{text}}}

OPLL B' (R U2 R' U' R U2 L' U R' U' L) B

Name: B(J-r)
Used in: ZBLL,OPLL
Optimal moves: (Jb+3)HTM
{{{text}}}

OPLL R' (R U2 R' U' R U2 L' U R' U' L) U' R


R-Perms

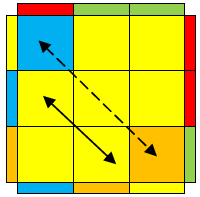
Name: B(R-r)
Used in: ZBLL,OPLL
Optimal moves: (Ra+2)HTM
{{{text}}}

OPLL R (U' L2 F' L' U' L' U L F L U2 L' U2 L) R'

Name: B(R-l)
Used in: ZBLL,OPLL
Optimal moves: (Rb+2)HTM
{{{text}}}

OPLL L' (U R2 F R U R U' R' F' R U2 R' U2 R) L


T-Perms

Name: B(T-f)
Used in: ZBLL, OPLL
Optimal moves: (T+2)HTM
{{{text}}}

OPLL F (R U R' U' R' F R2 U' R' U' R U R' F') F'

Name: B(T-b)
Used in: ZBLL, OPLL
Optimal moves: (T+2)HTM
{{{text}}}

OPLL B' (R U R' U' R' F R2 U' R' U' R U R' F') B

OPLL

Bowtie Cases | Headlight Cases | Chameleon Cases | Other Cases| edit

Headlights Cases

Y-perms

Name: H(Y-f)
Used in: ZBLL,OPLL
Optimal moves: (Y+2)HTM
{{{text}}}

OPLL F2 R U' R' U' R U R' F' R U R' U' R' F R F2

Name: H(Y-r)
Used in: ZBLL,OPLL
Optimal moves: (Y+2)HTM
{{{text}}}

OPLL R' F R U' R' U' R U R' F' R U R' U' R' F R F' R

Name: H(Y-fr)
Used in: ZBLL,OPLL
Optimal moves: (Y+2)HTM
{{{text}}}

OPLL F R' F R U' R' U' R U R' F' R U R' U' R' F R F' R F'


V-perms

Name: H(V-l)
Used in: ZBLL,OPLL
Optimal moves: (V+2)HTM
{{{text}}}

OPLL L' R' U R' U' y x R' F R' F' R2 U' R' U R U L

Name: H(V-f)
Used in: ZBLL,OPLL
Optimal moves: (V+2)HTM
{{{text}}}

OPLL F R' U R' U' y x R' F R' F' R2 U' R' U R U F'


N-Perms

Name: H(N-f)
Used in: ZBLL,OPLL
Optimal moves: (Na+2)HTM
{{{text}}}

OPLL F R' U R2 B2 U R' B2' R U' B2 R2' U' R F'

Name: H(N-b)
Used in: ZBLL,OPLL
Optimal moves: (Na+2)HTM
{{{text}}}

OPLL B R' U R2 B2 U R' B2' R U' B2 R2' U' R B'

Name: H(Nb-f)
Used in: ZBLL,OPLL
Optimal moves: (Nb+2)HTM
{{{text}}}

OPLL F' R' U R U' R' F' U' F R U R' F R' F' R U' R F

Name: H(Nb-b)
Used in: ZBLL,OPLL
Optimal moves: (Nb+2)HTM
{{{text}}}

OPLL B' R' U R U' R' F' U' F R U R' F R' F' R U' R B

Name: H(N-l)
Used in: ZBLL,OPLL
Optimal moves: (Na+2)HTM
{{{text}}}

OPLL L R' U R2 B2 U R' B2' R U' B2 R2' U' R U2 L'

Name: H(N-r)
Used in: ZBLL,OPLL
Optimal moves: (Na+2)HTM
{{{text}}}

OPLL U R2 B2 U R' B2' R U' B2 R2' U' R U2 L' U2 R'

Name: H(Nb-l)
Used in: ZBLL,OPLL
Optimal moves: (Nb+2)HTM
{{{text}}}

OPLL L' R' U R U' R' F' U' F R U R' F R' F' R U' R U2 L

Name: H(Nb-r)
Used in: ZBLL,OPLL
Optimal moves: (Nb+2)HTM
{{{text}}}

OPLL R2 U R U' R' F' U' F R U R' F R' F' R U' R U2 R


A-Perms

Name: H(A-l)
Used in: ZBLL,OPLL
Optimal moves: (Aa+2)HTM
{{{text}}}

OPLL L' R' F R' B2 R F' R' B2 R2 L

Name: H(B-r)
Used in: ZBLL,OPLL
Optimal moves: (Aa+2)HTM
{{{text}}}

OPLL F R' B2 R F' R' B2 R


J-Perms

Name: H(J-f)
Used in: ZBLL,OPLL
Optimal moves: (Jb+2)HTM
{{{text}}}

OPLL F' R U R' F' R U R' U' R' F R2 U' R' F

Name: H(L-f)
Used in: ZBLL,OPLL
Optimal moves: (Ja+2)HTM
{{{text}}}

OPLL F (y) R' U L' U2 R U' R' U2 L R U2 F'


G-Perms

Name: H(Ga-f)
Used in: ZBLL,OPLL
Optimal moves: (Ga+2)HTM
{{{text}}}

OPLL F' (y) R2' u R' U R' U' R u' R2 y' R' U R F

Name: H(Gc-f)
Used in: ZBLL,OPLL
Optimal moves: (Gc+2)HTM
{{{text}}}

OPLL F (y) R2' u' R U' R U R' u R2 y R U' R' F'

OPLL

Bowtie Cases | Headlight Cases | Chameleon Cases | Other Cases| edit

Chameleon Cases

T-perms

Name: C(T-lru)
Used in: ZBLL,OPLL
Optimal moves: (T+2)HTM
{{{text}}}

OPLL L' R U R U R' U' R' F R2 U' R' U' R U R' F' U' L' R

J-perms

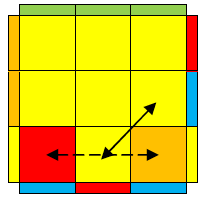
Name: C(J-lb)
Used in: ZBLL,OPLL
Optimal moves: (Jb+2)HTM
{{{text}}}

OPLL L' B' R U R' F' R U R' U' R' F R2 U' R' U' L B

Name: C(L-rb)
Used in: ZBLL,OPLL
Optimal moves: (Ja+2)HTM
{{{text}}}

OPLL R B (y) R' U L' U2 R U' R' U2 L R U' B' R'

OPLL

Bowtie Cases | Headlight Cases | Chameleon Cases | Other Cases| edit

Other Cases

Name: Q(F-fr)
Used in: ZBLL,OPLL
Optimal moves: (F+2)HTM
I Know this is a bad alg, but is does work for this case

OPLL F (R' U2 R' U2 L U' R' U' R' U R U2 L' U2 R U R) F


OPLL

Bowtie Cases | Headlight Cases | Chameleon Cases | Other Cases| edit

Retrieved from "https://www.speedsolving.com/wiki/index.php?title=OPLL&oldid=24506"