Christopher Mowla
Premium Member
Hello everyone,
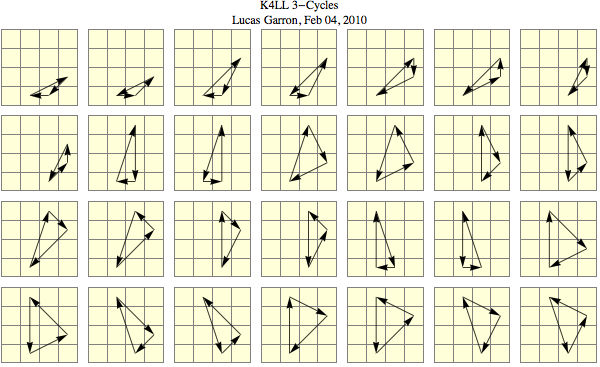
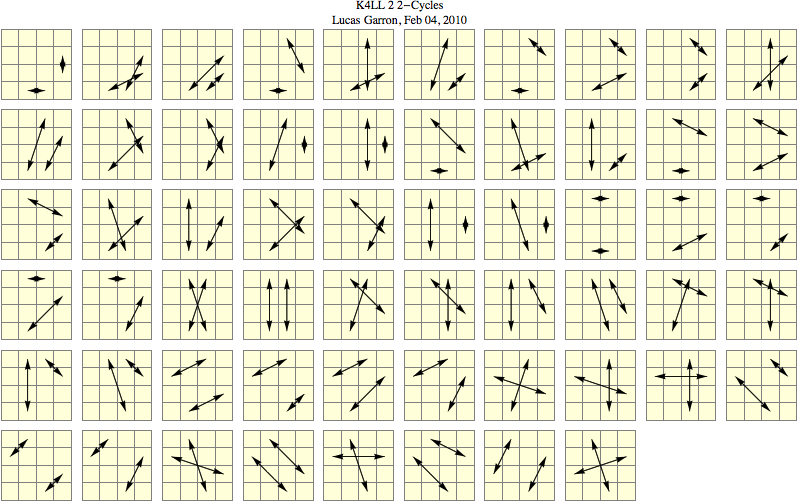
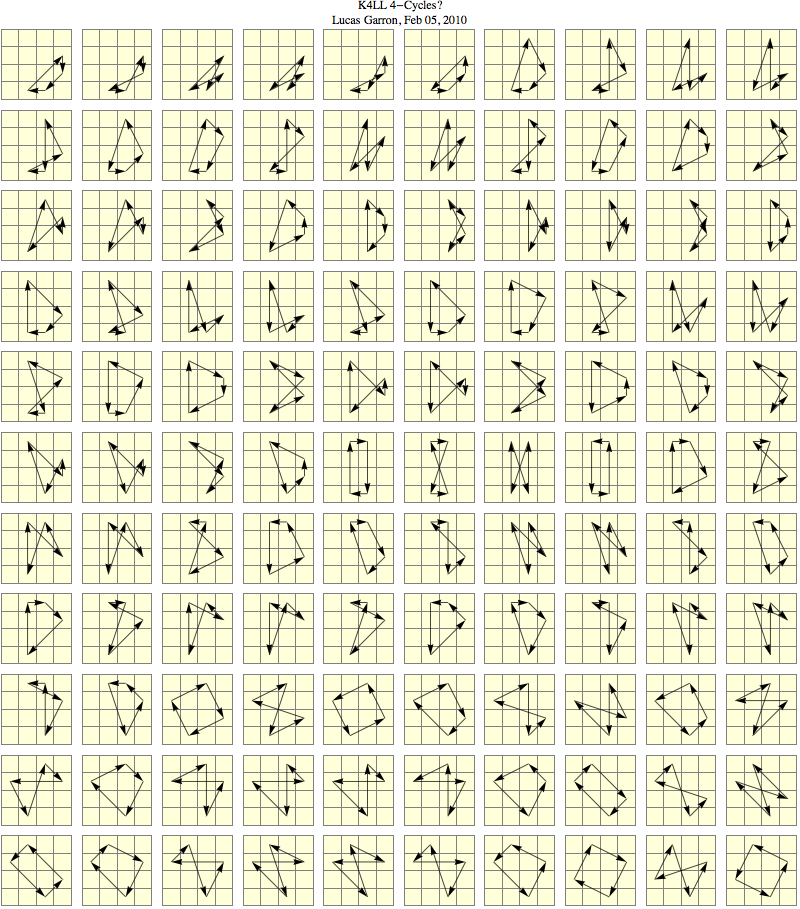
I have made a document which shows why there are exactly 28 distinct cases for 3-cycles of winged edges restricted in the last layer of a 4X4X4 or 5X5X5 cube.
I know that many have known that there are 28 cases for a long time now (just as I have known, even before looking at Thom Barlow's webpage), but I wanted to introduce another (interesting) way to verify why there are 28 cases.
In the document, I also include an organized table of all 28 cases which may be useful for those just beginning to learn the K4 method. There are two of these tables: one is with Thom Barlow's algorithms, and the other is a table without any algorithms (for custom algorithms).
I have made a document which shows why there are exactly 28 distinct cases for 3-cycles of winged edges restricted in the last layer of a 4X4X4 or 5X5X5 cube.
I know that many have known that there are 28 cases for a long time now (just as I have known, even before looking at Thom Barlow's webpage), but I wanted to introduce another (interesting) way to verify why there are 28 cases.
In the document, I also include an organized table of all 28 cases which may be useful for those just beginning to learn the K4 method. There are two of these tables: one is with Thom Barlow's algorithms, and the other is a table without any algorithms (for custom algorithms).
Attachments
Last edited: